
Thus, the angles of the isosceles triangle are 65º, 65º, and 50º.Borrowed from Late Latin isoscelēs, borrowed from Greek isoskelḗs "having equal legs, (of a triangle) having two equal sides, (of numbers) divisible into equal parts, even," from iso- iso- + -skelēs, adjective derivative of skélos (neuter s-stem) "leg," going back to an Indo-European base *skel- "bent," whence also Armenian šeł "slanting, crooked" with o-grade, Greek skoliós "bent, crooked, askew, devious" perhaps with a velar extension Germanic *skelga-/*skelha-, whence Old English sceolh "oblique, wry," Old Frisian skilich "squinting," Old High German skelah "crooked, oblique," Old Icelandic skjalgr "wry, oblique" The other angles can be considered as x each as they are equal. For example: Let the unequal angle of an isosceles triangle be 50º.
Now, if the measure of the third (unequal) angle is given, then the three angles can be added to equate it to 180º to find the value of x that gives all the angles of a triangle. The angles opposite to the equal sides of an isosceles triangle are considered to be an unknown variable 'x'. The angles of an isosceles triangle add up to 180º according to the angle sum property of a triangle.
DEFINITION OF AN ISOSCELES TRIANGLE HOW TO
How to find Angles using Isosceles Triangle Theorem? The two triangles now formed with altitude as its common side can be proved congruent by AAS congruence followed by proving the sides opposite to the equal angles to be equal by CPCT. An isosceles triangle can be drawn, followed by constructing its altitude. The converse of the isosceles triangle theorem can be proved by using the congruence properties and properties of an isosceles triangle. How to Prove the Converse of the Isosceles Triangle Theorem? The converse of isosceles triangle theorem states that, if two angles of a triangle are equal, then the sides opposite to the equal angles of a triangle are of the same measure. What is the Converse of Isosceles Triangle Theorem? The two triangles now formed with altitude as its common side can be proved congruent by SSS congruence followed by proving the angles opposite to the equal sides to be equal by CPCT.

Isosceles triangle theorem can be proved by using the congruence properties and properties of an isosceles triangle. Isosceles triangle theorem states that, if two sides of an isosceles triangle are equal then the angles opposite to the equal sides will also have the same measure. Related ArticlesĬheck these articles related to the concept of the isosceles triangle theorem.įAQs on Isosceles Triangle Theorem What is Isosceles Triangle Theorem? Hence we have proved that, if two angles of a triangle are congruent, then the sides opposite to the congruent angles are equal. Proof: We know that the altitude of a triangle is always at a right angle with the side on which it is dropped. Let's draw a triangle with two congruent angles as shown in the figure below with the markings as indicated. Converse of Isosceles Triangle Theorem Proof

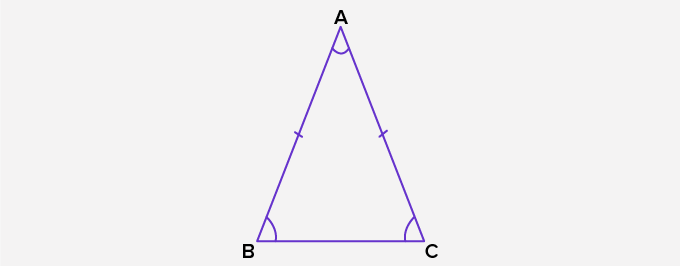
We will be using the properties of the isosceles triangle to prove the converse as discussed below. This is exactly the reverse of the theorem we discussed above. The converse of isosceles triangle theorem states that if two angles of a triangle are congruent, then the sides opposite to the congruent angles are equal. Hence, we have proved that if two sides of a triangle are congruent, then the angles opposite to the congruent sides are equal. Proof: We know, that the altitude of an isosceles triangle from the vertex is the perpendicular bisector of the third side. Given: ∆ABC is an isosceles triangle with AB = AC.Ĭonstruction: Altitude AD from vertex A to the side BC. Let's draw an isosceles triangle with two equal sides as shown in the figure below. To understand the isosceles triangle theorem, we will be using the properties of an isosceles triangle for the proof as discussed below. Isosceles triangle theorem states that if two sides of a triangle are congruent, then the angles opposite to the congruent sides are also congruent.


 0 kommentar(er)
0 kommentar(er)
